Monthly Archives: February 2016

by ZoMeu

AurumQ-1

In this article I’ll give you my method in order to solve the AurumQ-1 puzzle, a “bandaged ” 3x3x3.

For details, take a look at this page: http://www.twistypuzzles.com/cgi-bin/puzzle.cgi?pkey=2337

 

I made mine with cubetwist’s bandaging kit, so it doesn’t shapeshift, but apart from it, it does every moves an original would do and has the same “bandaging”.

Below you can find a scheme of the aurumQ-1 if you’d like to make your own one (you don’t need the kit to do it, only a simple 3x3x3 with a bit of tape is enough)

 

My solution is very simple and requires only 2 algorithms and a bit of intuition.

I splitted this method in 2 main parts:

aurumQ-1

aurumQ-1 taken from twistypuzzle’s museum

  • Corners pairing and placement

  • Edges placement

step 1: corners

So, as I just wrote, the first step will be to pair corners 2 by 2 (by pair I mean placing one corner next to it’s neighboor).

The 3 first pairs are purely intuitive, if you’ve already solved a 3x3x3 you shouldn’t have much troubles doing it.

The first problem may come at your fourth and last pair. Effectively, most of the time you’ll get the 2 last corners swapped. (if it is not the cast, you’re very lucky and can go to the next step)
The problem is that you can’t use algorithms like some PLLs of the CFOP method for standard 3x3x3s because your bandaged cube won’t allow some of the movements required.

So the solution has been to find another algorithm that does this action using only the allowed moves. I finally came to a solution, but I imagine it isn’t the most efficient algorithm to perform this task, if someone has better, feel free to share it in the comments.

In order to reverse them, I do the following algorithm (using the standard 3x3x3 notation) with my “middle-moving” slice on the left of my front face:

L2 U L2 U’ L2 D L2 U’ L2 U’ L2 U L2 U L2 U’ D’

After performing that, your last 2 corners should be nicely paired.

Maybe you’ll have seen at this step that we won’t have to look at the orientation of the corners, which makes the resolution even smaller.

You’re half done!

The next and last step will be to place your edges correctly!

step 2: edges

In order to place my edges, I’ve had again to create a new algorithm, the ones I knew couldn’t be applied due (again) to the bandaging.

The algorithm I made is not the best because it does 2 2 corners commutation, but it is enough to solve entirely the puzzle (this method doesn’t aim to speedsolve)

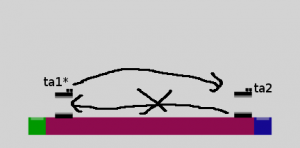
Assuming you’re in the same position as for the algorithm I wrote before, here are the edges that will be swapped:

  • {(front;up),(back;up)}
  • {(top;right),(bottom;left)}

Here is the algorithm:

L2 U (L2 U2)2 L2 U’ L2 U2 L2 U2

Try to think a bit and your puzzle will be solved within a few algorithms.

You’re now done, congratz 😛

This was very funny to figure out how to solve it. Obviously this isn’t a very efficient method but it is enough to feel proud of it!

by ZoMeu

EP – Unidirectionnal TP

Copy from an article I made a while ago on another place.

 

Unidirectionnal teleportation will allow you to create teleporters that leads it’s pair, but only in one direction (instead of both directions).

To make one, you just need to modify a bit the tags of your teleporters.

 

Name the first one as you would normally do (t+label+(1 or 2)) example: ta2

Then the second teleporter’s name will be a bit different. You must name if  as a normal other, but you will also add another character at the end, for example: ta1*

Then, you’ll be able to travel from ta1* to ta2 but not from ta2 to ta1*!

monodirectionnal tp scheme

visual explanations

 

 

Explanations:

Knowing how to do this is funny, but not as much as understanding it.

This the point of this part.

So, in order to understand why does it work, I opened the game with the software JPEXS Free Flash Decompiler, and searched through the code to find this function:

code to initialize tp

code to initialize tp

 

As you can see by it’s name, this function aims to initialize tps, pairing each one with it’s twin.

As you (already I think) now, to label a teleporter, you use the character ‘t’ followed by another character which will be the id of the teleporter, and finally, you use character 1 or 2 to inform if the teleporter is an entry/exit.

In the code, the id letter is registered in this.letter and the type in this.type.

The important fact to remark is that the substr function will only take the 3rd letter as type and no more.

Then comes the conditionnal structures which are used to pair the entry teleporter with it’s exit.

What is written there is:

  • if the type of your teleporter (this.type) equals to 1, then it’s partner’s label will be ‘t’+this.letter+’2′
  • if the type of your teleporter (this.type) equals to 2, then it’s partner’s label will be ‘t’+this.letter+’1′

These conditions allow us to create tps that are linked with another in only one direction.

If you didn’t understand, let’s take a look at a small example:

Let the first tp’s label be “ta1*” and the second “ta2”

During the init function these will be the values:

this.letter = ‘a’ // the id of our teleporter is here

this.type = ‘1’  // only the third character, the ‘*’ isn’t here

and at the end of the first if:

this.partner = “ta2”

This is totally normal, but when “ta2” will be initialized, it’s partner will switch to “ta1” and not “ta1*”

There you are, I hope you found it interesting!